In 2014-15, Dr. Kenneth Bollen co-chaired a National Science Foundation committee on replicability in the social, behavioral, and economic sciences. This report leaves little doubt that we have a problem: it is far more difficult to replicate prior research than it should be. Though there are many contributing causes, it is clear that we need to develop more robust and reliable methods for research. Many common statistical models and estimation techniques in psychology and other sciences assume we have the true model and that our variables come from normal distributions. Yet, uncertainty about our model selection and non-normality of our variables are the norm rather than the exception and lead to biased estimates and inaccurate tests of our scientific hypotheses.
For some time now, Dr. Bollen has been developing ways to estimate models that are more robust to these problems. The model below illustrates these points. This is a path diagram of a Structural Equation Model (SEM) where by convention the ovals represent latent variables, meaning that they cannot be observed directly. Latent variables represent abstract concepts such as intelligence, attitudes, happiness, and the numerous other psychological variables for which we have only imperfect measures. The indicators or measures of latent variables appear in boxes. The remaining variables are the error variables, either measurement errors or errors in the latent variable equation. Single headed straight arrows represent a direct effect from the variable at the base of the arrow to the variable to which it points. The vertical and horizontal dashed lines with the short arrows signify a correlation among all the errors that they connect.
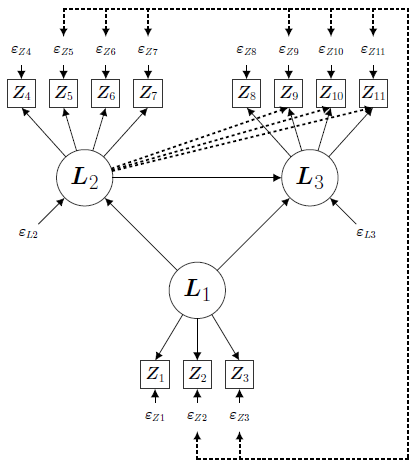
Suppose that the true model included all solid and dashed lines and the model the researcher mistakenly uses omits the dashed lines. For example, the dashed lines from L2 to Z9 to Z11 represent that these L3 indicators are contaminated by L2. The other dashed lines show that the errors for most of the measures are correlated with each other due to omitted factors. Assume our primary interests are in testing the hypotheses about the relationships between the latent variables. There are no errors in this part of the model: causal relationships are correctly specified. Because the usual estimator for SEM estimates all relationships simultaneously, however, it spreads biases from one part of the model to even the correctly specified parts. In this instance, mistakes in the measurement part of the model lead to biases in estimating relationships among the latent variables. To deal with this problem, Dr. Bollen has developed Model Implied Instrumental Variable (MIIV) estimators that are more robust to such specification errors. When combined with a Two Stage Least Squares (2SLS) estimator, it is referred to as MIIV-2SLS. The MIIV-2SLS estimator applied to the latent variable model (L2 and L3 equations) in this mis-specified path diagram would still recover unbiased coefficients of the latent variable relationships despite the extensive errors resulting from omitting the associations represented by the dashed lines. In addition, the MIIV-2SLS is robust to non-normality.
Dr. Bollen has joined forces with Dr. Kathleen Gates, an Assistant Professor of Quantitative Psychology, and graduate student Zack Fisher to apply this estimator to fMRI data where there is much uncertainty about the linkages between different brain regions and hence much room for error. The research team is developing empirical techniques based on MIIV-2SLS to help identify the connections. This team also is furthering our understanding of when the MIIV-2SLS is robust to errors and when it is not. One such result is that the MIIV-2SLS estimation of the measurement model is robust to virtually all mistakes in the latent variable model. Another paper led by Mr. Fisher applies the MIIV-2SLS estimator to dynamic factor analysis with time series data. MIIVsem, an R program implements many of these procedures. Furthermore, Michael Giordano, also a graduate student in Quantitative Psychology, is developing MIIV-2SLS methods for multilevel models. In addition, Dr. Bollen has developed MIIV-2SLS methods for testing the dimensionality of constructs and is working with David Braudt, a Sociology graduate student, on this project.
Moreover, Dr. Bollen is working with Dr. Silvia Bianconcini, an Italian statistician, to develop a general longitudinal model that encompasses a diverse set of longitudinal models as special cases. This is intended to provide a robust modeling framework so that researchers can turn to simpler models when permissible and more comprehensive models when needed. Ai Ye, another graduate student in the Quantitative Psychology Program, is developing a Monte Carlo simulation study to see how well these general models can discriminate between different panel models.
All these projects are designed to be more forgiving of the uncertainty and mistakes in modeling we inevitably make and to contribute to a more robust and reliable science.

Dr. Kenneth Bollen is the Henry Rudolph Immerwahr Distinguished Professor in the Quantitative Psychology Program within the Department of Psychology and Neuroscience at UNC Chapel Hill. He also holds a joint appointment with the Department of Sociology, is the head of the Methodology Core, and a Fellow at the UNC Carolina Population Center. Learn more about his research online.

